Le fonctionnement du perceptron

Les réseaux de neurones ont permis des avancées majeures dans des domaines divers. Ils sont à la base du fonctionnement des systèmes de reconnaissances faciales, ils permettent de catégoriser des objets de manière précise et ils peuvent même devenir artistes ou médecins (presque).

Toutes ces avancées nous font parfois oublier que les mathématiciens ont délaissés les réseaux de neurones pendant de longues décennies.

Il faut savoir que la théorie sous-jacente existe depuis les années 50. Jusqu’en 2010, les réseaux de neurones avaient enchainé des phases ou tout le monde était impressionnés par ce qu’ils pourraient permettre de faire, et des phases ou ils étaient oubliés et parfois même critiqués sévèrement.

Naissance et évolution du perceptron

Tout commence dans les années 50, quand deux neurologues Warren McCulloch et Walter Pitts souhaitent modéliser informatiquement le fonctionnement d’un neurone biologique (on le sait peu mais la biologie a beaucoup apporté aux mathématiques).

De façon simple, un neurone formel est un objet mathématique qui prend une entrée donnée et renvoi une sortie binaire : 0 ou 1.

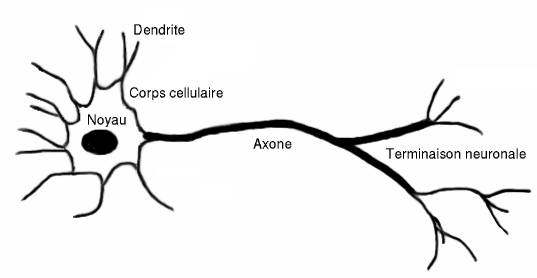
Le concept de neurone en mathématiques est une modélisation simpliste du fonctionnement d’un neurone humain. Un neurone humain est une cellule composées : de synapses, de dendrites, d’un corps cellulaire et d’un axone.

Les dendrites sont les entrées du neurone, les axones leurs sorties, c’est eux qui assurent la connexion avec les autres neurones.

Le corps cellulaire va se charger de réguler l’activation du neurone en réponse aux intensités électriques des signaux excitateurs. L’activation s’effectue lorsque le potentiel d’action est au-dessus d’un seuil appelé potentiel d’activation.

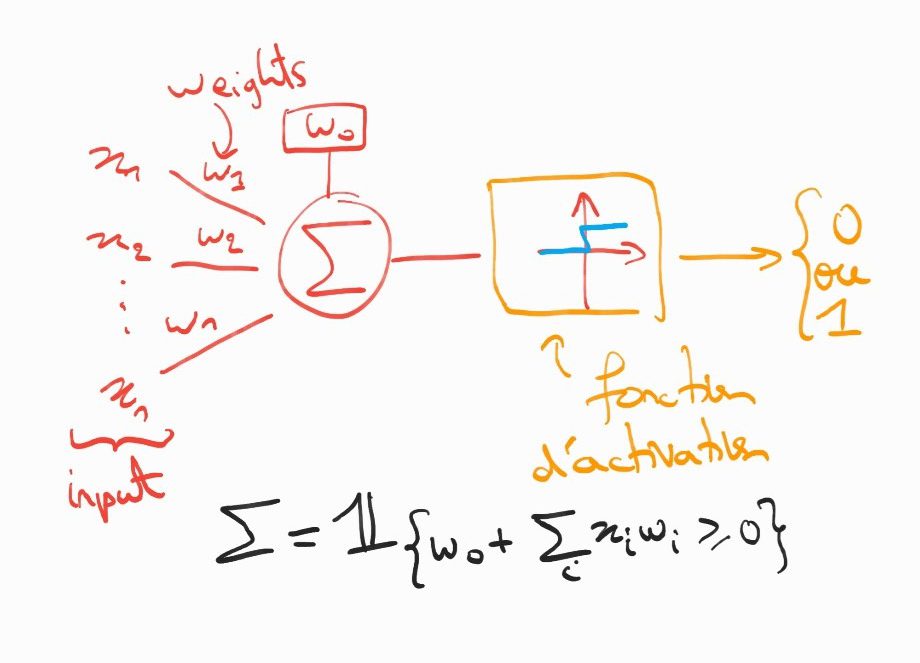
Par analogie, un neurone artificiel est un objet mathématiques qui ‘’s’active’’ si la combinaison linéaire de ses entrées, appelées input, avec les poids w1,…,wn est supérieure à un certain seuil fixé par l’opérateur.

Perceptron pour la régression logistique

Cette approche permet par exemple de résoudre des problèmes de classification binaire. On considère que l’on a un certain nombre d’observations que l’on peut représenter par le nuage de points suivant :

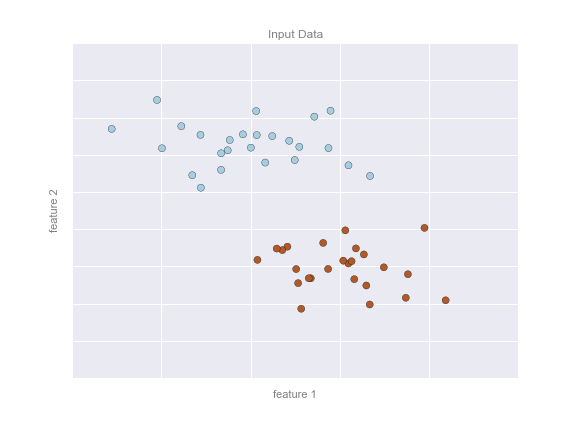
On voit clairement que deux groupes se forment et on cherche une droite linéaire optimale pour les séparer. Pour faire ça on peut se servir du perceptron (même si d’autres méthodes plus efficaces existent et ce n’est pas le perceptron qui est utilisé en pratique).

Le principe est le suivant :

• On sépare nos points en deux ensembles, un ensemble de test et un ensemble d’entrainement.
• L’objectif est de trouver les poids w, qui vont minimiser une fonction de perte qui est définie (de façon schématique) comme la distance entre la droite et les points. On prend souvent la loss cross entropy comme indicateur de l’erreur.
• A l’état initial, les w sont choisis de façon aléatoire, puis à chaque étape ils sont recalculés (par une méthode d’optimisation de type gradient par exemple) jusqu’à ce que l’on ait une entropie assez faible.

Même si aujourd’hui le perceptron n’est plus utilisé pour des applications concrètes en entreprise, il est en pratique un des pères du deep learning.